水晶振動子について:水晶振動子
水晶振動子
1. 振動モードと切断方位
図1は、ATカット振動モードについて常温付近における周波数温度特性の1次温度係数が零となるカットアングルを模式的に表したものです。
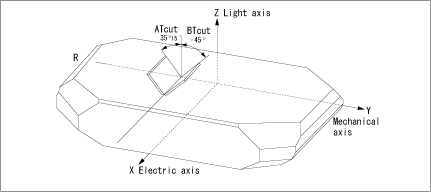
図1 Z板人工水晶における切断方位
また、図2はATカット(基本波)の厚みすべり振動の振動形態を模式的に表したものです。
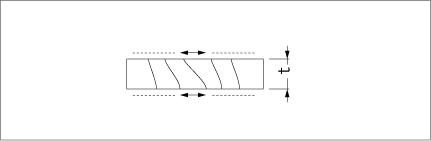
図2 振動形態(ATカットの基本波)
表1は、一般に使用されているATカットの対応周波数範囲、周波数定数(素板厚と周波数の関係)を示してあります。
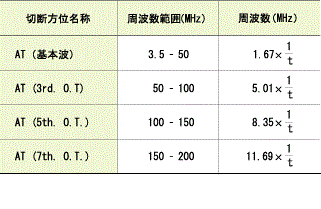
表1 ATカットの周波数の関係
2. 切断方位と周波数温度特性
水晶の周波数温度特性は、その曲線の形状から2 種類に分けられます。
1つは、3次曲線、もう1つは、2次曲線です。図3は、ATカットの特性例を示しています。
AT カット振動子は、常温付近での温度変化に対する周波数変化が少なく最も広く使用されています。
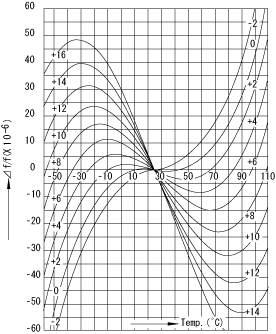
図3 ATカットの周波数温度特性例
3. 等価回路と各定数
水晶振動子は、共振周波数の近傍において、図5 に示す等価回路として表すことが出来ます。
ここで、
R1 :等価直列抵抗(Series Resistance)
L1 :等価直列インダクタンス(Motional Inductance)
C1 :等価直列容量(Motional Capacitance)
C0 :並列容量(Shunt Capacitance)
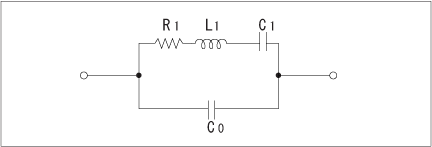
図5 水晶振動子の等価回路
図6は、共振周波数の近傍における水晶振動子のアドミタンス円線図と、振動子の等価回路です。
各回路条件での等価回路の様子と周波数、抵抗などの関係がわかります。ここで、各定数は、次の関係があります。
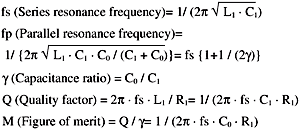
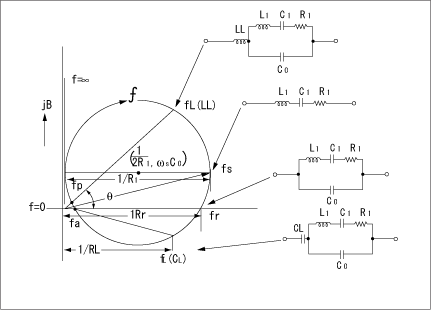
図6 アドミタンス円線図
